Рентгеновский лазер на свободных электронах

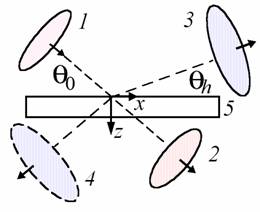
1 – падающий лазерный рентгеновский импульс, 2 - прошедший импульс, 3 - отраженный импульс в случае Брэгга и в случае Лауэ (4), 5 - монокристалл.

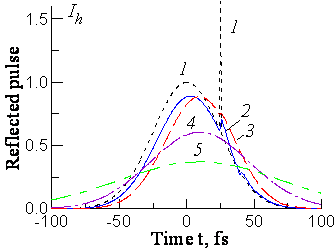
Эффект дифракционного расплывания и “обрезания” рентгеновского импульса. 1 - падающий импульс, состоящий из двух импульсов с t₀₁ = 50 фс и t₀₂ = 0.5 фс, радиус импульса r₀ = 100 mm; 2 - отраженный импульс; 3 - отраженный импульс при r₀ = 10 mm и z = 0; z = 1 м (4) и z = 2 м (5). Геометрия Брэгга, l = 0.154 нм, b = 1, Si(220), толщина кристалла d = 5 mm.

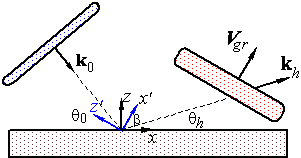
Иллюстрация необычного эффекта отличия направлений фазовой и групповой скоростей отраженного импульса в вакууме случае несимметричной дифракции.

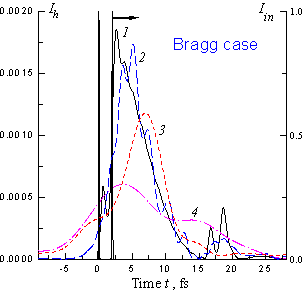
Дифракционное отражение двух импульсов с длительностями t₀ = 0.1 фс. Расстояние от кристалла z (см): 1 - 0, 2 - 2, 3 - 10, 4 - 20. Случай Брэгга, b = 2, l = 0.154 нм, Si(220), d = 4 mm.

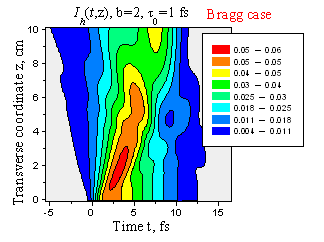
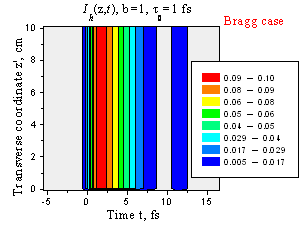
Пространственно-временное распределение интенсивности отраженного импульса с длительностью t₀ = 1 фс. Случай Брэгга, 1 - b = 1, 2 - b = 2.

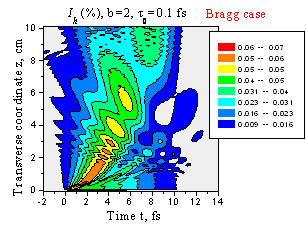
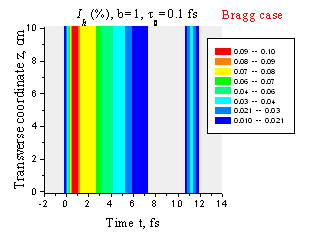
Пространственно-временное распределение интенсивности отраженного сверхкороткого импульса при t₀ = 0.1 фс. Случай Брэгга, 1 - b = 1, 2 - b = 2.

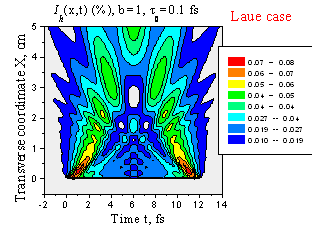
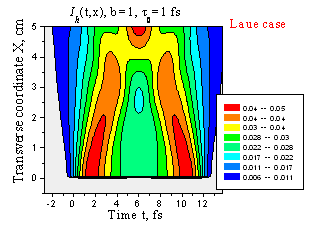
Пространственно-временное расплывание отраженного лазерного импульса при t₀ = 1 фс (a) и t₀ = 0.1 фс (b). Геометрия Лауэ, b = 1, l = 0.154 нм, Si(220), d = 7.7 mm.

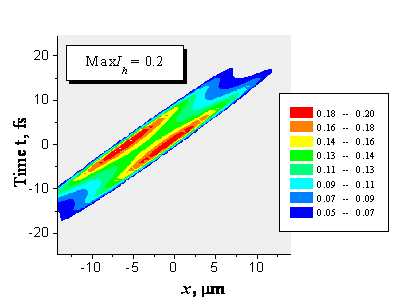
Эффект расщепления отраженного импульса в случае Лауэ при падении гауссова импульса с радиусом r₀ = 10 mm, длительность импульса t₀ = 1 фс (l = 0.154 нм, Si(220), z = d = 7.7 mm).

            В группе проф. В.А. Бушуева совместно с учеными из Германии проводятся теоретические исследования в области дифракции импульсов РЛСЭ в кристаллах и многослойных структурах для управления временной (продольной) когерентностью этих импульсов (гранты РФФИ № 10-02-00768, № 12-02-00924) и BMBF Project 05K10CHG). Одной из серьезнейших проблем является учет неоднородного и нестационарного нагрева кристаллов под действием сверхмощных рентгеновских импульсов.

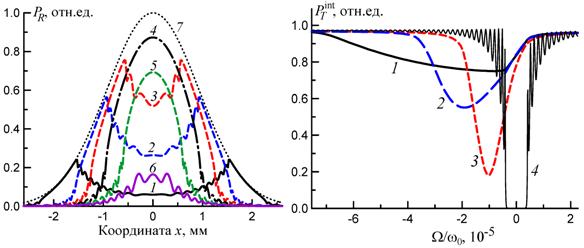
                                   Рис. 1                                                                                    Рис. 2

Рис. 1. Интегральные коэффициенты отражения P_R(x) при e = -2 (1), -3 (2), -3.5 (3), -4 (4), -4.5 (5) и e = –5 (6); 7 – профиль интенсивности I₀(x, 0, z), начальная температура T₀ = 200 K, время от начала падения пачки импульсов t = 600 мкс. Кристалл алмаза толщиной 100 мкм, отражение (400).

Рис. 2. Интегральные кривые дифракционного прохождения при начальных температурах кристалла T₀ = 300 K (1), 200 K (2) и 150 K (3); 4 – кривая прохождения для идеального кристалла.

            Интенсивности R- и T-импульсов зависят от времени, координаты и спектральной отстройки e = W/DW_B, где DW_B – спектральная ширина отражения от идеального кристалла (рис. 1). Наличие неоднородного температурного поля приводит к уменьшению интегрального (по x, y и t) коэффициента прохождения, к его уширению, асимметрии и к смещению минимума в отрицательную область спектра (рис. 2). Кроме того, очень необычным по сравнению с “холодным” кристаллом является пространственное по поверхности кристалла распределение интенсивности отражения (рис. 3), что необходимо будет учитывать при проведении соответствующих экспериментов.

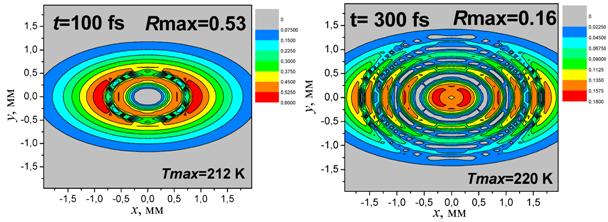
Рис. 3. Карта распределения интенсивности отражения I_R(x, y) в области спектра e = -3 в моменты времени 100 и 300 фс.